

A video game company launches an exciting new advertising campaign. They predict the number of online visits to their website, or hits, will double each day. The model they are using shows \(2\) hits the first day, \(4\) hits the second day, \(8\) hits the third day, and so on (Table \(\PageIndex\)).
| Day | 1 | 2 | 3 | 4 | 5 | … |
|---|---|---|---|---|---|---|
| Hits | 2 | 4 | 8 | 16 | 32 | … |
If their model continues, how many hits will there be at the end of the month? To answer this question, we’ll first need to know how to determine a list of numbers written in a specific order. In this section, we will explore these kinds of ordered lists.
One way to describe an ordered list of numbers is as a sequence. A sequence is a function whose domain is a subset of the counting numbers. The sequence established by the number of hits on the website is
The ellipsis (…) indicates that the sequence continues indefinitely. Each number in the sequence is called a term. The first five terms of this sequence are \(2\), \(4\), \(8\), \(16\), and \(32\).
Listing all of the terms for a sequence can be cumbersome. For example, finding the number of hits on the website at the end of the month would require listing out as many as \(31\) terms. A more efficient way to determine a specific term is by writing a formula to define the sequence.
One type of formula is an explicit formula, which defines the terms of a sequence using their position in the sequence. Explicit formulas are helpful if we want to find a specific term of a sequence without finding all of the previous terms. We can use the formula to find the nth term of the sequence, where nn is any positive number. In our example, each number in the sequence is double the previous number, so we can use powers of 2 to write a formula for the nth term.

The first term of the sequence is \(2^1=2\), the second term is \(2^2=4\), the third term is \(2^3=8\), and so on. The nth term of the sequence can be found by raising 2 to the nth power. An explicit formula for a sequence is named by a lower case letter \(a\), \(b\), \(c\). with the subscript \(n\). The explicit formula for this sequence is
Now that we have a formula for the nth term of the sequence, we can answer the question posed at the beginning of this section. We were asked to find the number of hits at the end of the month, which we will take to be 31 days. To find the number of hits on the last day of the month, we need to find the 31 st term of the sequence. We will substitute 31 for \(n\) in the formula.
If the doubling trend continues, the company will get \(2,147,483,648\) hits on the last day of the month. That is over \(2.1\) billion hits! The huge number is probably a little unrealistic because it does not take consumer interest and competition into account. It does, however, give the company a starting point from which to consider business decisions.
Another way to represent the sequence is by using a table. The first five terms of the sequence and the nth term of the sequence are shown in Table \(\PageIndex\).
| \(n\) | 1 | 2 | 3 | 4 | 5 | \(n\) | |
|---|---|---|---|---|---|---|---|
| \(n^ | \) term of the sequence, \(a_n\) | 2 | 4 | 8 | 16 | 32 | \(2^n\) |
Graphing provides a visual representation of the sequence as a set of distinct points. We can see from the graph in Figure \(\PageIndex\) that the number of hits is rising at an exponential rate. This particular sequence forms an exponential function.
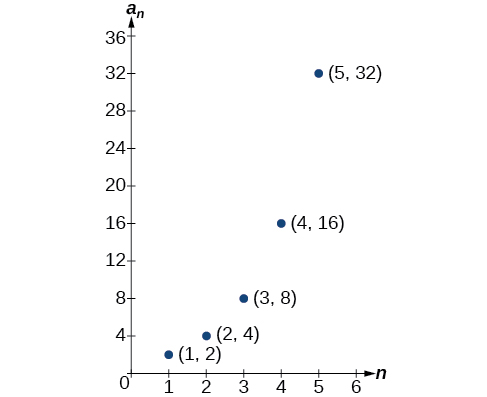
Figure \(\PageIndex\)
Lastly, we can write this particular sequence as
A sequence that continues indefinitely is called an infinite sequence. The domain of an infinite sequence is the set of counting numbers. If we consider only the first \(10\) terms of the sequence, we could write
This sequence is called a finite sequence because it does not continue indefinitely.
A sequence is a function whose domain is the set of positive integers. A finite sequence is a sequence whose domain consists of only the first \(n\) positive integers. The numbers in a sequence are called terms. The variable \(a\) with a number subscript is used to represent the terms in a sequence and to indicate the position of the term in the sequence.
We call \(a_1\) the first term of the sequence, \(a_2\) the second term of the sequence, \(a_3\) the third term of the sequence, and so on. The term \(a_n\) is called the nth term of the sequence, or the general term of the sequence. An explicit formula defines the nth term of a sequence using the position of the term. A sequence that continues indefinitely is an infinite sequence.
No. In certain problems, it may be useful to define the initial term as \(a_0\) instead of \(a_1\). In these problems, the domain of the function includes \(0\).
Write the first five terms of the sequence defined by the explicit formula \(a_n=−3n+8\).
Solution
Substitute \(n=1\) into the formula. Repeat with values \(2\) through \(5\) for \(n\).
\(\begin n=1 & a_1=−3(1)+8=5 \\ n=2 & a_2=−3(2)+8=2 \\ n=3 & a_3=−3(3)+8=−1 \\ n=4 & a_4=−3(4)+8=−4 \\ n=5 & a_5=−3(5)+8=−7 \end\)
The first five terms are \(\\).
Analysis
The sequence values can be listed in a table. A table, such as Table \(\PageIndex\), is a convenient way to input the function into a graphing utility.
| \(n\) | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| \(a_n\) | 5 | 2 | –1 | –4 | –7 |
A graph can be made from this table of values. From the graph in Figure \(\PageIndex\), we can see that this sequence represents a linear function, but notice the graph is not continuous because the domain is over the positive integers only.

Figure \(\PageIndex\)
Write the first five terms of the sequence defined by the explicit formula \(t_n=5n−4\).
The first five terms are \(\\).
Sometimes sequences have terms that are alternate. In fact, the terms may actually alternate in sign. The steps to finding terms of the sequence are the same as if the signs did not alternate. However, the resulting terms will not show increase or decrease as \(n\) increases. Let’s take a look at the following sequence.
Notice the first term is greater than the second term, the second term is less than the third term, and the third term is greater than the fourth term. This trend continues forever. Do not rearrange the terms in numerical order to interpret the sequence.
Write the first five terms of the sequence.
Solution
Substitute \(n=1\), \(n=2\), and so on in the formula.
Analysis
The graph of this function, shown in Figure \(\PageIndex\), looks different from the ones we have seen previously in this section because the terms of the sequence alternate between positive and negative values.

Figure \(\PageIndex\)
Yes, the power might be \(n\), \(n+1\), \(n−1\), and so on, but any odd powers will result in a negative term, and any even power will result in a positive term.
Write the first five terms of the sequence: